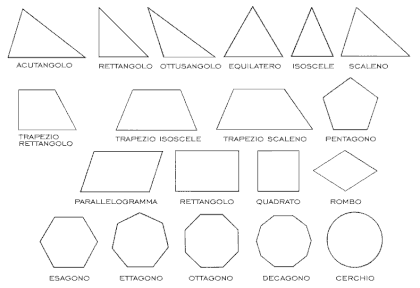
Figure piane
Poligoni
Il poligono è una superficie delimitata da una linea spezzata chiusa.
Il termine deriva dal greco e significa (poly=molti e gònos=angolo).
I segmenti che la compongono si definiscono lati, i punti di incontro dei lati si chiamano vertici.
Nella geometria i poligoni più studiati sono i regolari, cioè quelli con angoli e lati uguali.
Triangoli
La somma degli angoli interni di un triangolo è di 180°, questi possono essere:
- equilatero: tutti gli angoli (60°) e i lati uguali;
- isoscele: due lati e uguali;
- rettangolo: con 1 angolo retto (90°)
- scaleno: tutti gli angoli e, di conseguenza, i lati diversi.
Quadrilateri
La somma degli angoli interni di un quadrilatero è di 360° (il doppio di 1 triangolo), questi possono essere:
- quadrato: tutti i lati e gli angoli uguali (90°);
- rettangoli: tutti gli angoli uguali (90°) e i lati due a due uguali;
- rombo: tutti gli angoli e i lati due a due uguali;
- parallelogrammo: tutti i lati tra loro paralleli e gli angoli due a due uguali;
- trapezio: tutti gli angoli e, di conseguenza, i lati diversi.
Poligoni regolari
Un poligono si dice regolare se ha tutti gli angoli e i lati uguali, si può sempre inscrivere in una circonferenza, che passa per tutti i suoi vertici.
Si chiama apotema la distanza tra il centro del poligono e uno dei lati, l’apotema deve formare con il lato un angolo di 90°.
Ogni poligono prende il nome dal numero di lati e angoli:
- triangolo: 3 angoli;
- quadrilatero: 4 angoli;
- pentagono: 5 angoli;
- esagono: 6 angoli;
- ettagono: 7 angoli;
- ottagono: 8 angoli;
- enagono: 9 angoli;
- decagono: 10 angoli;
- endecagono: 11 angoli;
- dodecagono: 12 angoli;
gli altri poligoni non hanno nomi particolari e si indicano con: poligono con 13 lati, 14, ecc.
Cerchio
Il cerchio è tutta la superficie compresa all’interno della circonferenza.
La circonferenza è una linea curva chiusa formata da un’insieme di punti che hanno tutti la stessa distanza dal centro.
Pi greco
il π (pi greco) viene definito come il rapporto tra la lunghezza della circonferenza e quella del suo diametro, o anche come l'area di un cerchio di raggio 1.
π = c/d = c/2r = 3,14
Il π è un numero puro (adimensionale), conosciuto anche come costante di Archimede e il suo valore (troncato alla 100ª cifra decimale) è:
3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679
Per facilità il suo valore viene arrotondato a: 3,14
La misura della circonferenza è pari al raggio moltiplicato per 2π (r x 6,28).
π=c/d =3,14 d= diametro
Possiamo definire i seguenti elementi:
- raggio: segmento che unisce un punto qualsiasi della circonferenza con il centro;
- diametro: segmento che unisce due punti qualsiasi della circonferenza passando per il centro;
- corda: segmento che unisce due punti qualsiasi della circonferenza non passando per il centro;
- arco: parte della circonferenza compresa tra due suoi punti;
- tangente: retta che tocca la circonferenza in un solo punto, la sua distanza dal centro è pari al raggio, con cui forma un angolo retto;
- secante: retta che interseca la circonferenza in 2 punti
- semicirconferenza: la metà della circonferenza.
 Tecnologia
Tecnologia